- Blog
- Wissenschaften
- Sinus, Kosinus, Tangens und Kotangens –...
Trigonometrie: Sinus, Kosinus, Tangens und Kotangens
Hier sind einige Tipps, die Ihnen das Abitur erleichtern. Noch nie war es so einfach, Nachhilfe für das Abitur zu nehmen!
Die trigonometrischen Funktionen sind mathematische Funktionen, die die Winkel eines Dreiecks mit seinen entsprechenden Seiten in Beziehung setzen. Mit gezielter Nachhilfe in Mathe kannst du sie jedoch im Handumdrehen verstehen!

Mathe-Nachhilfe in deiner Nähe
Inhaltsverzeichnis
Einleitung
Die trigonometrischen Funktionen sind mathematische Funktionen, die die Winkel eines Dreiecks mit seinen entsprechenden Seiten in Beziehung setzen. Spätestens im Matheunterricht im Gymnasium wirst du dich mit ihnen beschäftigen müssen.
Sie spielen eine wichtige Rolle in der Mathematik, Physik, Ingenieurwissenschaften und anderen Bereichen, in denen die Analyse von Winkeln und periodischen Phänomenen erforderlich ist.
Arten von trigonometrischen Funktionen
Es gibt verschiedene Arten von trigonometrischen Funktionen:
- Sinus (sin): Die Sinusfunktion beschreibt das Verhältnis der Länge der dem Winkel gegenüberliegenden Seite zu der Hypotenuse in einem rechtwinkligen Dreieck.
- Kosinus (cos): Die Kosinusfunktion beschreibt das Verhältnis der Länge der anliegenden Seite zu der Hypotenuse in einem rechtwinkligen Dreieck.
- Tangens (tan): Die Tangensfunktion beschreibt das Verhältnis der Länge der dem Winkel gegenüberliegenden Seite zu der anliegenden Seite in einem rechtwinkligen Dreieck.
- Kotangens (cot): Die Kotangensfunktion ist der Kehrwert des Tangens und beschreibt das Verhältnis der Länge der anliegenden Seite zu dem Winkel gegenüberliegenden Seite in einem rechtwinkligen Dreieck.
MERKE: Es gibt verschiedene Arten davon, darunter Sinus (sin), Kosinus (cos), Tangens (tan) und Kotangens (cot). Sie können durch einen Kreis, den sogenannten Einheitskreis, dargestellt werden, der ein nützliches Werkzeug beim Studium der Trigonometrie darstellt und es ermöglicht, die Werte der Funktionen zu analysieren und sie für jeden Winkel zu berechnen. Es wird grafisch wie folgt dargestellt:
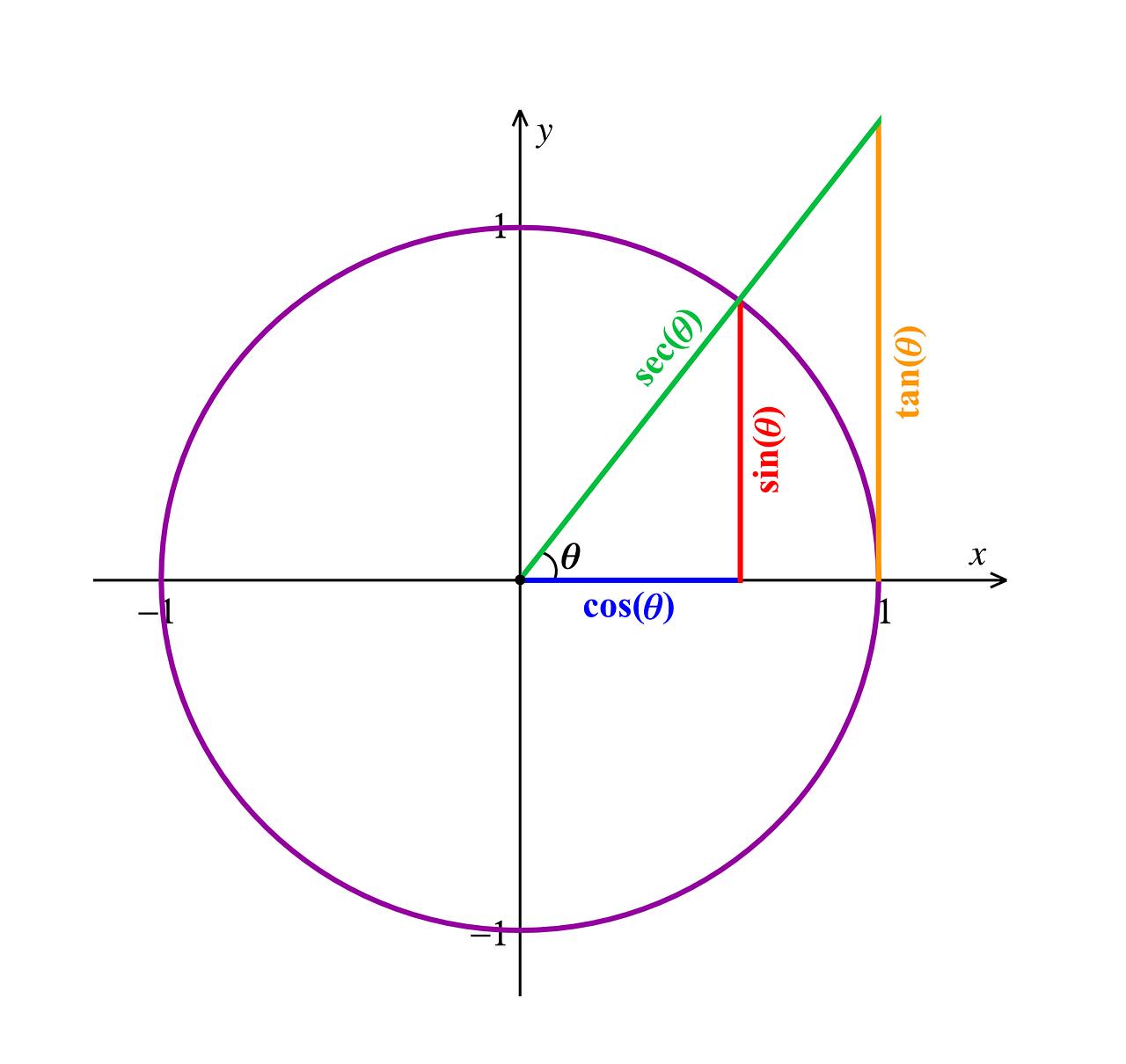
Dort finden wir 4 Viertel von jeweils 90°, die zusammen einen vollständigen Kreis von 360° bilden.
Der Sinus
Der Sinus (sin) eines Winkels wird definiert als das Verhältnis zwischen der dem Winkel gegenüberliegenden Kathete und der Länge der Hypotenuse. Im Kontext des Einheitskreises wird der Sinus eines Winkels jedoch als die y-Koordinate des Punktes auf dem Einheitskreis dargestellt, der dem Winkel entspricht.
Für Schülerinnen und Schüler, die ihre mathematischen Fähigkeiten auf Gymnasialniveau verbessern möchten, ist es oft hilfreich, gezielte Mathe-Nachhilfe für das Gymnasium zu suchen.
Der Sinus eines Winkels hat beobachtbare und leicht identifizierbare Eigenschaften, zu denen Folgendes gehört:
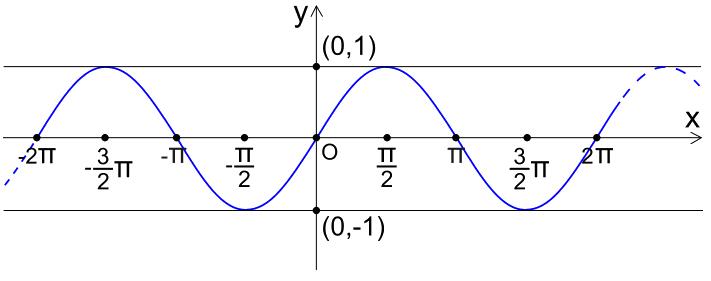
- Periodizität: Der Sinus ist eine periodische Funktion mit einer Periode von 2π Radianten oder 360°. Das bedeutet, dass er sich alle 360° wiederholt, was leicht durch den Sinusgrafen dargestellt werden kann.
- Wertebereich: Der Sinus eines Winkels kann Werte zwischen -1 und +1 annehmen, da der Kreis einen Radius von 1 hat.
- Ungerade Symmetrie: Sinus ist eine ungerade Funktion. Dies bedeutet, dass der Sinusgraf symmetrisch zur Ursprungsgeraden ist.

Der Einheitskreis
Grafische Darstellung durch den Einheitskreis:
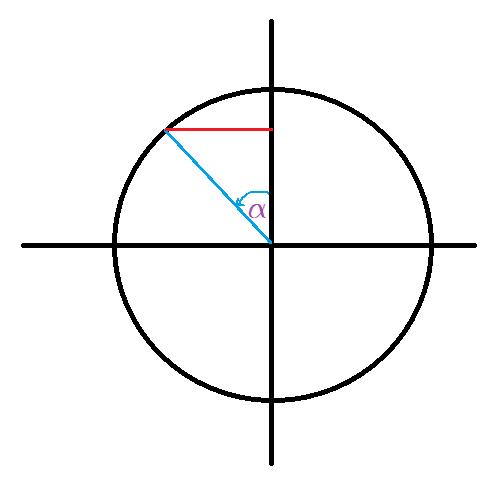
Daher ist der Sinus des Winkels a wie folgt:
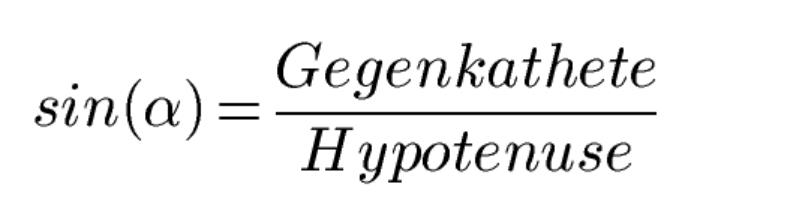
Der Cosinus
Der Kosinus (cos) eines Winkels wird definiert als das Verhältnis zwischen der dem Winkel benachbarten Kathete und der Länge der Hypotenuse. Diese Definition kann auf alle Winkel in der Ebene erweitert werden, indem der Begriff des Einheitskreises verwendet wird.
Vielen Schüler:innen bereitet der Kosinus Kopfschmerzen, mit gezielter Nachhilfe in Mathe, können viele Sorgen erspart werden und unsere Nachhilfelehrer:innen können dir den Einheitskreis in deinem Tempo erklären!
Im Kontext des Einheitskreises wird der Kosinus eines Winkels jedoch als die x-Koordinate des Punktes auf dem Einheitskreis definiert, der dem Winkel entspricht.
Der Kosinus eines Winkels weist beobachtbare und leicht identifizierbare Eigenschaften auf, zu denen Folgendes gehört:
- Periodizität: Der Kosinus ist eine periodische Funktion mit einer Periode von 2π Radianten oder 360°. Das bedeutet, dass er sich alle 360° wiederholt, was leicht durch den Kosinusgrafen dargestellt werden kann.
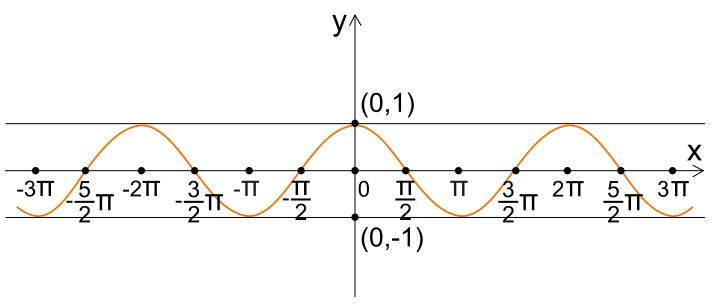
- Wertebereich: Der Kosinus eines Winkels kann Werte zwischen -1 und +1 annehmen, da der Kreis einen Radius von 1 hat.
- Gerade Symmetrie: Der Kosinus ist eine gerade Funktion, was bedeutet, dass der Kosinusgraf symmetrisch zur y-Achse ist.
Hier findest du Nachhilfe fürs Abitur in deiner Nähe
Grafische Darstellung durch den Einheitskreis:
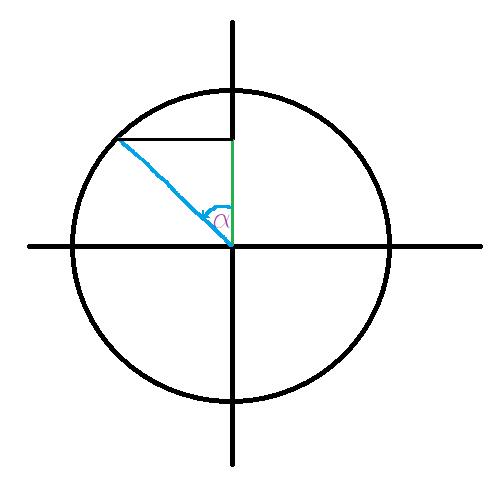
Daher ist der Kosinus des Winkels a wie folgt:
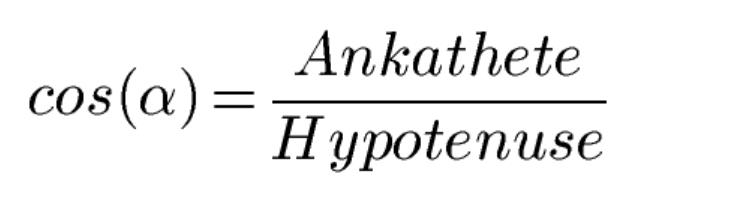
Der Tangens
Tangens (tan): Er wird definiert als das Verhältnis zwischen Sinus und Kosinus eines Winkels. Der Tangens eines Winkels hat beobachtbare und leicht identifizierbare Eigenschaften, darunter:
-
Nicht durch 0 (null) teilbar: Der Tangens ist nicht definiert, wenn der Kosinus den Wert Null hat.
-
Periodizität: Der Tangens hat eine Periode von π Radianten oder 180°. Das bedeutet, dass er sich alle 180° wiederholt, was leicht durch den Tangensgrafen dargestellt werden kann.
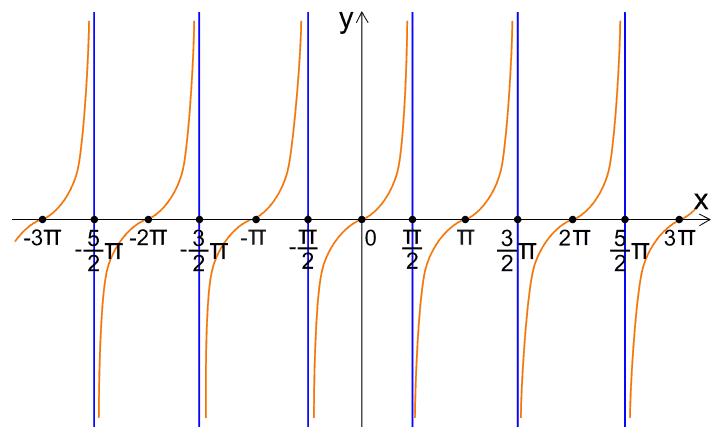
- Wertebereich: Tangens nimmt Werte zwischen minus unendlich und plus unendlich an.
- Ungerade Symmetrie: Es zeigt eine ungerade Funktion im Graphen.
Grafische Darstellung durch den Einheitskreis:
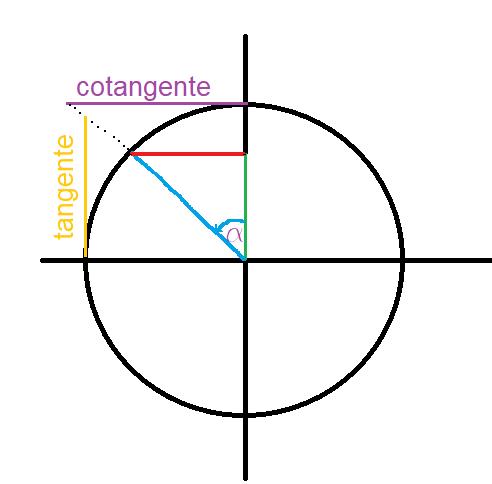
Daher ist der Tangens des Winkels a wie folgt:
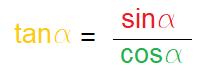
Der Kotangens
Kotangens (cot): Er ist eine der trigonometrischen Funktionen und das Reziprok des Tangens eines Winkels. Definiert wird er als das Verhältnis zwischen dem Kosinus und dem Sinus des Winkels.
Um den Kotangens grafisch darzustellen, muss die Funktion cot (a) in Abhängigkeit von a gezeichnet werden. Der Kotangens ist eine periodische Funktion mit vertikalen Asymptoten an den Stellen, wo der Sinus 0 (null) ist. Erfahre, wie du Asymptoten richtig erkennst!
Diese Asymptoten entsprechen den Winkeln im Dreieck, für die die gegenüberliegende Seite gleich 0 (null) ist, also den Vielfachen von π.
Der Kotangens eines Winkels hat beobachtbare und leicht identifizierbare Eigenschaften, darunter:
-
Nicht durch 0 (null) teilbar: Der Kotangens ist nicht definiert, wenn der Sinus des Winkels null ist.
-
Periodizität: Er hat eine Periodizität von 180°, was leicht durch den Kotangensgrafen dargestellt werden kann.

- Wertebereich: Der Kotangens kann reale Werte zwischen minus unendlich und plus unendlich annehmen.
- Ungerade Symmetrie: Der Kotangens ist eine ungerade Funktion.
Grafische Darstellung durch den Einheitskreis:
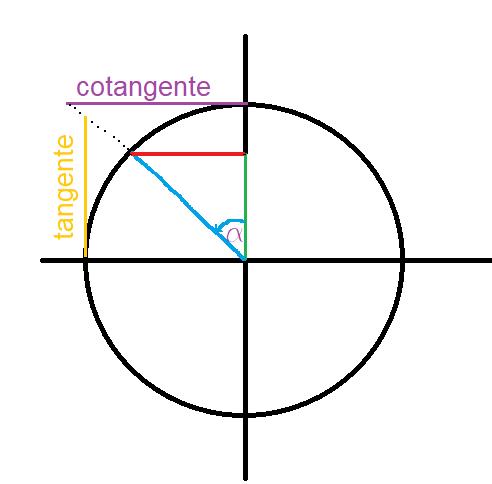
Daher ist der Kotangens des Winkels a wie folgt:
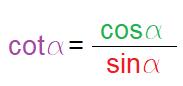
Der Kotangens wird in verschiedenen mathematischen, physikalischen und ingenieurwissenschaftlichen Bereichen verwendet und ist eine wichtige trigonometrische Funktion, die Informationen über das Verhältnis der Seiten eines rechtwinkligen Dreiecks liefert und verwendet wird, um eine Vielzahl von theoretischen und praktischen Problemen zu lösen.
Fazit
Die trigonometrischen Funktionen sind entscheidend, um die Beziehung zwischen den Winkeln eines Dreiecks und den entsprechenden Seiten zu verstehen. Sie sind in vielen Bereichen wie Mathematik, Physik und Ingenieurwissenschaften unverzichtbar.
Die verschiedenen Funktionen wie Sinus, Kosinus, Tangens und Kotangens haben jeweils spezifische Eigenschaften und Anwendungen. Durch gezielte Nachhilfe in Mathe kannst du schnell ein Verständnis für diese Funktionen entwickeln und ihre Anwendungen in verschiedenen Bereichen meistern.
Wenn du deine mathematischen Fähigkeiten verbessern möchtest, findest du hier entsprechende Unterstützung in deiner Nähe oder online!